Cara Mudah Menentukan Tanda pada Garis Bilangan dalam Menyelesaikan Pertidaksamaan - Tips Marthen Kanginan

Dalam menyelesaikan suatu pertidaksamaan, membuat garis bilangan adalah salah satu tahapan yang perlu kita lakukan, terutama jika pertidaksamaan tersebut memiliki beberapa titik kritis atau pembuat nol seperti pertidaksamaan polynomial atau pertidaksamaan rasional . Secara umum, berikut inilah tahapan-tahapan dalam menyelesaikan pertidaksamaan:

1. Jadikan ruas kanan pertidaksamaan bernilai $0$
2. Faktorkan / tentukan titik kritis (pembuat nol)
3. Buat garis bilangan
4. Tentukan tanda $+$ atau $-$ setiap interval pada garis bilangan
5. Tentukan himpunan penyelesaian.

Untuk pertidaksamaan linear dan pertidaksamaan kuadrat, masih dapat dengan mudah kita selesaikan bahkan tanpa membuat garis bilangan. Namun untuk pertidaksamaan yang memuat beberpa faktor atau memiliki banyak titik kritis, membuat garis bilangan menjadi hal yang perlu untuk kita lakukan dalam menentukan himpunan penyelesaian, seperti pertidaksamaan berikut ini:

$\displaystyle x^2 \left(2x-3\right)^3 \left(x-3\right)^2 \left(2x-7\right)\lt 0$

Pertidaksamaan di atas, memiliki $4$ titik kritis, yaitu $x=0$, $x=\frac{3}{2}$, $x=3$ dan $x=\frac{7}{2}$, sehingga jika kita buat garis bilangannya sebagai berikut:

Seperti kita lihat pada garis bilangan di atas, $4$ titik kritis menyebabkan terbentuknya lima buah interval (daerah) yang perlu kita uji tanda pada masing-masing interval apakah $+$ atau $-$. Jika kita lakukan pengujian dengan mengambil sembarang titik uji pada masing-masing interval, misalnya pada interval I $(x\lt 0)$ kita ambil $x=-1$ sebagai titik uji, pada interval II $(0\lt x\lt \frac{3}{2})$ kita ambil $x=1$ sebagai titik uji, bagaimana dengan interval IV $\left( 3\lt x\lt \frac{7}{2}\right)$? tentunya kita tidak bisa mengambil $x$ bilangan bulat sebagai titik uji, tentu ini akan cukup "merepotkan". Berikut ini tips cara mudah menentukan tanda $+$ atau $-$ pada garis bilangan tanpa menggunakan titik uji.

  Tips Marthen Kanginan

Bagi yang berkecimpung di "dunia" matematika dan fisika pasti sudah tidak asing dengan nama Marthen Kanginan, sudah banyak buku karya beliau yang beredar dan memberikan kontribusi yang sangat besar untuk pendidikan di negeri ini, sama halnya seperti penulis besar lainnya seperti Pak Sukino (salah satu ide kreatif pak Sukino adalah Horner-Kino ), Pak Suwah Sembiring, Pak Husein Tampomas dan penulis lainnya yang sudah memberikan ide dan karya luar biasa untuk kita manfaatkan, semoga kesehatan selalu menyertai beliau semua (saya rekomendasikan anda membeli buku karya-karya beliau, InsyaAlloh sangat bermanfaat).

Salah satu tips yang di berikan pak Marthen Kanginan adalah bagaimana cara mudah menentukan tanda $+$ atau $-$ pada garis bilangan dalam menyelesaiakan pertidaksamaan tanpa menggunkan titik uji. Berikut ini langkah-langkah tips Marthen Kanginan :

   Tips Marthen Kanginan

Cara mudah menentukan tanda pada garis bilangan dengan langkah-langkah sebagai berikut:

  Tentukan tanda pada daerah paling kanan hanya dengan mengalikan koefisien $x$ dari tiap-tiap fakor

Untuk daerah (interval lainnya), gunakan aturan sebagai berikut: "ketika melewati titik kritis, tanda bergantian kecuali ketika melewati titik kritis yang berasal dari $x^2$ atau $(ax+b)^2$ atau $(ax+b)^n$ dengan $n$ genap maka tanda tetap.

Sebagai contoh, kita akan menyelesaikan pertidaksamaan yang tadi, sebagai berikut:

$\displaystyle x^2 \left(2x-3\right)^3 \left(x-3\right)^2 \left(2x-7\right)\lt 0$

Dari pertidaksamaan di atas, kita peroleh titik kritis $x=0$, $x=\frac{3}{2}$, $x=3$ dan $x=\frac{7}{2}$, maka garis bilangannya sebagai berikut:

Langkah pertama dari tips Marthen Kanginan adalah kita tentukan tanda pada interval paling kanan, dalam soal ini berarti interval V. Tanda pada interval paling kanan ditentukan oleh koefisien dari masing-masing variable $x$ setiap faktor. Maka kita peroleh:

$(x^2)(2x)(x)(2x)=$ Positif

Maka daerah paling kanan bernilai positif $(+)$

Berikutnya, kita tentukan tanda pada interval lainnya dengan aturan jika melewati titik kritis yang berasal dari faktor berpangkat genap, maka tanda tetap. 

Pada pertidaksamaan di atas,

$\frac{7}{2}$ berasal dari $(2x-7)$ (pangkat ganjil) maka ketika melewati $\frac{7}{2}$ tanda berubah
$3$ berasal dari $(x-3)^2$ (pangkat genap) maka ketika melewati $3$ tanda tetap
$\frac{3}{2}$ berasal dari $(2x-3)^3$ (pangkat ganjil) maka ketika melewati $\frac{3}{2}$ tanda berubah
$0$ berasal dari $x^2$ (pangkat genap), maka ketika melewati $0$ tanda tetap

untuk lebih jelasnya perhatikan garis bilangan berikut

Maka penyelesaian pertidaksamaan $x^2(2x-3)^3(x-3)^2(2x-7)\lt 0 $ adalah daerah dengan tanda negatif karena pertidaksamaan memiliki tanda $\lt 0$ (negatif), maka penyelesaiannya seperti ditunjukkan oleh gambar berikut:

Yaitu: $\displaystyle\frac{3}{2}\lt x\lt 3$ atau $\displaystyle 3\lt x\lt\frac{7}{2}$

Untuk lebih jelas, perhatikan beberapa contoh lain berikut ini:

Contoh 1

Tentukan penyelesaian dari pertidaksamaan $(x-1)(x-2)^2(x-3)^3(x-4)\leq 0$

Jawab:

Titik kritis pertidaksamaan di atas adalah $x=1$, $x=2$, $x=3$, dan $x=4$. Interval paling kanan positif, titik kritis yang berasal dari faktor dengan pangkat genap adalah $x=2$, dengan demikian tanda tidak berubah ketika melewati $x=2$ maka garis bilangannya adalah:

Bulatan pada garis bilangan "penuh/berisi" karena, tanda pada pertidaksamaan $\leq 0$ memuat tanda sama dengan, artinya titik kritis termasuk penyelesaian. Jadi, penyelesaian dari pertidaksamaan $(x-1)(x-2)^2(x-3)^3(x-4)\leq 0$ adalah $x\leq 1$ atau $3\leq x\leq 4$

---

Contoh 2

Tentukan penyelesaian dari $\displaystyle\frac{(x-1)(x-2)^3}{(x-3)^2(x-4)}\geq 0$

Jawab:

Titik kritis pertidaksamaan di atas adalah $x=1$, $x=2$, $x=3$ dan $x=4$. Tanda pada interval paling kanan positif, karena koefisien semua variabel $x$ positif. Titik kritis yang berasal dari faktor pangkat genap adalah $x=3$, dengan demikian tanda tidak berubah ketika melewati $x=3$.

Meskipun tanda pada pertidaksamaan memuat sama dengan $(\geq 0)$, namun untuk titik kritis yang berasal dari penyebut diberi "bulatan kosong", artinya titik kritis tersebut tidak termasuk penyelesaian.

Jadi, penyelesaian dari pertidaksamaan $\displaystyle\frac{(x-1)(x-2)^3}{(x-3)^2(x-4)}\geq 0$ adalah $1\leq x\leq 2$ atau $x\gt 4$

---

Contoh 3

Tentukan penyelesaian dari pertidaksamaan $x^2(2x^2-x)\lt x^2(2x+5)$  

Jawab:

\begin{align*}x^2(2x^2-x)-x^2(2x+5)&\lt 0\\ x^2((2x^2-x)-(2x+5))&\lt 0\\x^2(2x^2-3x-5 )&\lt 0\\x^2(2x-5)(x+1)&\lt 0\end{align*}

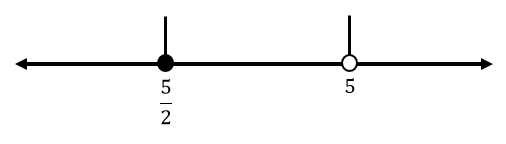
Titik kritis $x=0$, $x=\frac{5}{2}$ dan $x=-1$. Tanda pada interval paling kanan positif. Titik kritis yang berasal dari faktor dengan pangkat genap adalah $x=0$, maka ketika melewati $x=0$ tanda tidak berubah.

Jadi, penyelesaian dari pertidaksamaan $x^2(2x^2-x)\lt x^2(2x+5)$ adalah $-1\lt x\lt 0$ atau $0\lt x\lt \frac{5}{2}$

Jika anda masih belum paham, sebaiknya lihat video pembahasannya disini

Demikianlah cara mudah menentukan tanda $+$ atau $-$ garis bilangan dengan tips Marthen Kanginan. Semoga bermanfaat.

Untuk latihan pertidaksamaan secara online bisa anda coba soal berikut ini

Cara Menyelesaikan Pertidaksamaan Rasional atau Pertidaksamaan Pecahan (Matematika Wajib kelas X)

Pertidaksamaan rasional adalah  pertidaksamaan yang berbentuk pecahan dengan pembilang dan penyebut memuat variabel atau hanya penyebutnya saja yang memuat variabel. Berikut ini beberapa contoh pertidaksamaan rasional.

$\displaystyle\frac{2x-1}{x+3}\geq 0$

$\displaystyle\frac{x^2-1}{x+7}\leq 5$

$\displaystyle\frac{5}{2x-1}\gt \frac{x+1}{x-5}$

Di atas, ada 3 contoh pertidaksamaan rasional atau pertidaksamaan pecahan dengan bentuk yang berbeda. Namun, bagaimanapun bentuknya, pertidaksamaan rasional selalu dapat diubah sehingga menjadi salah satu dari bentuk umum pertidaksamaan rasional sebagai berikut:

$\displaystyle\frac{f(x)}{g(x)}\lt 0$ atau $\displaystyle\frac{f(x)}{g(x)}\leq 0$

$\displaystyle\frac{f(x)}{g(x)}\gt 0$ atau $\displaystyle\frac{f(x)}{g(x)}\geq 0$

Dengan $f(x)$ sebagai fungsi pembilang dan $g(x)$ sebagai fungsi penyebut dan $g(x)\ne 0$.

Bagaimana Cara Menyelesaikan Pertidaksamaan Rasional?

---

Berikut ini beberapa langkah penyelesaian pertidaksamaan rasional atau pertidaksamaan pecahan:

Langkah-langkah penyelesaian pertidaksamaan rasional:

Ubah ruas kanan pertidaksamaan menjadi nol
 Jika fungsi pembilang atau fungsi penyebut berupa polinomial derajat lebih dari 1, maka faktorkan
 Cari titik kritis atau pembuat nol fungsi pembilang dan fungsi penyebut
 Gambar pada garis bilangan
 Lakukan pengujian daerah yang dibatasi titik kritis pada garis bilangan
 Tentukan himpunan penyelesaian

Perlu diingat bahwa penyebut tidak boleh bernilai nol, dengan demikian saat menggambar garis bilangan, titik kritis yang diperoleh dari penyebut selalu digambarkan dengan bulatan kosong, artinya titik tersebut tidak termasuk penyelesaian meskipun tanda pertidaksamaan pada soal memuat tanda sama dengan ($\leq$ atau $\geq$).

Contoh Soal dan Penyelesaian

---

Untuk lebih memahami cara menyelesaiakan pertidaksamaan rasional, perhatikan contoh soal dan pembahasan berikut ini.

Soal pertama yang akan kita selesaiakan adalah pertidaksamaan rasional berikut:

$\displaystyle\frac{5x-20}{x-5}\leq 3$

Langkah pertama, kita perlu menjadikan ruas kanan pada pertidaksamaan menjadi nol, yaitu dengan dengan mengurangi kedua ruas dengan $3$, kemudian sederhanakan bentuk pada ruas kiri dengan menyamakan penyebutnya

$\begin{align*}\frac{5x-20}{x-5}-3&\leq 3-3\\ \frac{5x-20}{x-5}-3&\leq 0 \\ \frac{5x-20}{x-5}-\frac{3(x-5)}{x-5}&\leq 0\\ \frac{5x-20-3x+15}{x-5}&\leq 0\\ \frac{2x-5}{x-5}&\leq 0\end{align*}$

Langkah kedua, kita tentukan titik kritis, yaitu pembuat nol pada pembilang dan penyebut.

Pembuat nol pada pembilang adalah $\displaystyle 2x-5=0\Leftrightarrow x=\frac{5}{2}$

Pembuat nol pada penyebut adalah $\displaystyle x-5=0\Leftrightarrow x=5$

Langkah ketiga, kita buat garis bilangan yang memuat beberapa daerah yang dibatasi oleh titik kritis yang kita peroleh dari langkah kedua, dan perlu diingat pada titik kritis yang diperoleh dari penyebut digambarkan dengan tanda bulatan kosong meskipun pertidaksamaan yang sedang kita selesaikan $\leq$.

Langkah keempat, tentukan tanda masing-masing daerah pada garis bilangan dengan melakukan pengujian.

Pada garis bilangan di atas, kita peroleh tiga daerah, yaitu $x\leq\frac{5}{2}$ kita sebut saja "daerah kiri",  daerah $\frac{5}{2}\leq x \lt 5$ kita sebut sebagai "daerah tengah" dan daerah $x\gt 5$ kita sebut sebagai "daerah kanan".

Pada masing-masing daerah tersebut kita ambil sembarang angka penguji, misal untuk daerah kiri $(x\leq \frac{5}{2})$ saya ambil $x=0$, untuk daerah tengah $(\frac{5}{2}\leq x\lt 5)$ saya ambil $x=3$, dan untuk daerah kanan $(x\gt 5)$ saya ambil $x=6$ sebagai penguji. Dengan mensubstitusi titik-titik penguji tersebut ke fungsi rasional $\displaystyle \frac{2x-5}{x-5}$ maka kita peroleh:

Titik Uji	$2x-5$	$x-5$	$\displaystyle\frac{2x-5}{x-5}$
$x=0$	$(-)$	$(-)$	$\frac{(-)}{(-)}=(+)$
$x=3$	$(+)$	$(-)$	$\frac{(+)}{(-)}=(-)$
$x=6$	$(+)$	$(+)$	$\frac{(+)}{(+)}=(+)$

Baca juga : Cara mudah menentukan tanda $+$ dan $-$ garis bilangan tanpa titik uji

kita peroleh

Langkah kelima, kita tentukan himpunan penyelesaian dengan kembali memperhatikan tanda pertidaksamaan dan tanda pada garis bilangan.

Pertidaksamaan $\displaystyle\frac{2x-5}{x-5}\leq 0$ memiliki tanda pertidaksamaan $\leq$, dengan demikian himpunan penyelesaiannya adalah yang bertanda negatif atau atau nol $(\leq 0)$, yaitu daerah tengah pada garis bilangan tadi.

maka himpunan penyelesaian dari pertidaksamaan $\displaystyle \frac{5x-20}{x-5}\leq 3$ adalah $\left\{x | \frac{5}{2}\leq x \lt 5, x\in R\right\}$

Masalah Pertidaksamaan Rasional Yang Memuat Faktor Persekutuan Pembilang dan Penyebut

---

Berikutnya, kita akan mencoba menyelesaiak pertidaksamaan berikut ini:
$$\frac{x^3-3x^2-8x-10}{x^2-3x-10}\lt 1$$

Dengan mengurangi kedua ruas dengan 1 kita peroleh:

$\begin{align*}\frac{x^3-3x^2-8x-10}{x^2-3x-10}-1&\lt 1-1\\ \frac{x^3-3x^2-8x-10}{x^2-3x-10}-1&\lt 0\\ \frac{x^3-3x^2-8x-10}{x^2-3x-10}-\frac{x^2-3x-10}{x^2-3x-10}&\lt 0\\ \frac{x^3-3x^2-8x-10-x^2+3x+10}{x^2-3x-10}&\lt 0\\ \frac{x^3-4x^2-5x}{x^2-3x-10}&\lt 0\end{align*}$

Berikutnya, kita faktorkan pembilang dan penyebut sehingga kita peroleh

$\displaystyle\frac{x(x+1)(x-5)}{(x+2)(x-5)}\lt 0$

Seperti yang kita lihat, terdapat faktor persekutuan pada pembilang dan penyebut, yaitu $(x-5)$, pada pertidaksamaan rasional faktor persekutuan tidak boleh kita sederhanakan atau bahkan kita hilangkan, hal yang umum dilakukan jika terdapat faktor persekutuan misalnya $(ax+b)$ maka kita kalikan dengan $(ax+b)^2$ yang sudah jelas positif dan tidak merubah tanda pertidaksamaan. Jadi, untuk pertidaksamaan di atas, kedua ruas kita kali dengan $(x-5)^2$ dengan $x\ne 5$ sehingga kita peroleh:

$\displaystyle\frac{x(x+1)(x-5)^2}{x+2}\lt 0$

titik kritis (pembuat nol) dari pembilang dan penyebut yang kita peroleh adalah: $x=0$, $x=-1$, $x=5$ dan $x=-2$, maka bisa kita buat garis bilangan sebagai berikut:

Dengan melakukan pengujian masing-masing daerah, kita peroleh tanda sebagai berikut:

tanda yang diminta pada pertidaksamaan terakhir adalah $\lt 0$ atau negatif, dipenuhi oleh daerah yang diarsir berikut:

maka himpunan penyelesaian pertidaksamaan $\displaystyle\frac{x^3-3x^2-8x-10}{x^2-3x-10}\lt 1$ adalah $\{x| x\lt -2\text{ atau }-1\lt x \lt 0, x\in R\}$


Masalah Pertidaksamaan Rasional yang Memuat Fungsi Definit

---

Secara bahasa, definit artinya pasti. Dalam matematika terutama yang berkaitan dengan fungsi kuadrat dikenal dua definit yaitu definit positif dan definit negatif. Definit positif artinya fungsi tersebut selalu menghasilkan nilai positif untuk setiap $x$ anggota bilangan real, dan definit negatif artinya fungsi selalu menghasilkan nilai negatif untuk setiap $x$ anggota bilangan real.

Fungsi kuadrat $y=ax^2+bx+c$ dikatakan definit positif jika $a\gt 0$ dan $b^2-4ac\lt 0$, maka untuk berapapun nilai $x$ anggota bilangan real, nilai $y$ selalu positif.

Fungsi kuadrat $y=ax^2+bx+c$ dikatakan definit negatif jika $a\lt 0$ dan $b^2-4ac\lt 0$, maka untuk berapapun nilai $x$ anggota bilangan real, nilai $y$ selalu negatif.

Perhatikan contoh pertidaksamaan rasional berikut:

Himpunan penyelesaian pertidaksamaan $\displaystyle\frac{(x-1)(2x+4)}{(x^2+4)}\lt 1$ adalah ....

Penyelesaian:

$\begin{align*}\frac{(x-1)(2x+4)}{(x^2+4)}-1&\lt 0 \\ \frac{(2x^2+2x-4)-(x^2+4)}{(x^2+4)}&\lt 0\\ \frac{x^2+2x-8}{x^2+4}&\lt 0\end{align*}$

Karena $x^2+4$ merupakan definit positif, maka kita hanya perlu memperhatikan pembilangnya saja.

$\begin{align*}x^2+2x-8&\lt 0\\(x+4)(x-2)&\lt 0\end{align*}$

Titik kritisnya adalah $x=-4$ dan $x=2$, maka garis bilangannya sebagai berikut:

Jadi, himpunan penyelesaian dari pertidaksamaan $\displaystyle\frac{(x-1)(2x+4)}{(x^2+4)}\lt 1$ adalah $\{x | -4\lt x\lt 2\}$

Jika anda sudah paham, silakan coba soal online pertidaksamaan rasional berikut sebagai bahan latihan. Semoga bermanfaat, demikianlah materi pertidaksamaan rasional kelas X matematika wajib.

Download Soal Dan Pembahasan UN (UNBK atau UNKP) Matematika SMP 2018 Paket 4

m4th-lab.net - Download Pembahasan Ujian Nasional (UN) Matematika SMP / MTs Tahun 2018 Paket 4

Sebelumnya, kami telah membagikan pembahasan Ujian Nasional (UN) Matematika SMP 2018 Paket 1 (Download disini ), dan pembahasan UN matematika SMP 2018 Paket 2  (Download disini ). Pada kesempatan ini kami akan membagikan pembahasan soal Ujian Nasional (UN) SMP/MTs tahun 2018 paket 4 (paket 3 masih dalam proses). Jika anda memerlukan soal UN SMP 2018 lengkap semua pelajaran silakan download disini

Tidak dapat dipungkiri, Nilai Rata-rata Ujian Nasional 2018 menurun dibandingkan dengan pelaksanaan Ujian Nasional (UN) tahun-tahun sebelumnya terutama pada pelaksanaan UNBK (Ujian Nasional Berbasis Komputer) yang sangat minim kemungkinan adanya kecurangan. Pada tahun 2016 sebanyak 680 sekolah SMP/MTs negeri/swasta melaksanakan UNBK dan memperoleh nilai rata-rata 65,05. Pada tahun 2017 sebanyak 8.882 sekolah SMP/MTs negeri/swasta sudah melaksanakan UNBK dan memeperoleh rata-rata nilai 55,51. Dan yang terbaru, pada tahun 2018 banyak sekolah SMP/MTs yang melaksanakan UNBK meningkat drastis, yaitu sebanyak  17.760 sekolah negeri/swasta namun nilai rata-rata mengalami penurunan yaitu 52,96.

Pada pelaksanaan Ujian Nasional tahun 2019 mendatang, Kementrian Pendidikan dan kebudayan menargetkan 100% sekolah sudah melaksanakan UNBK (sumber lihat di sini), dikhawatirkan dengan dilaksanakannya UNBK nilai UN tahun mendatang pun akan mengalami penurunan. Namun kita jangan berkecil hati, pelaksanaan UJian Nasional masih sangat lama, setidaknya kita bisa memperiapkan diri sedini mungkin.

Untuk mempersiapakan diri menghadapai Ujian Nasional (UNBK maupun UNKP) tahun 2019 mendatang, pada kesempatan ini m4th-lab akan membagikan salah satu paket (salah satu kode soal) soal dan pembahasan Ujian Nasional (UN) 2018 mata pelajaran matematika. Kami harap, soal dan pembahasan ini dapat membantu adik-adik kelas 9 untuk mempersiapkan diri menghadapi UN 2019 mendatang.



Soal yang kami bagikan ini merupakan soal UNKP (Ujian Nasional Berbasis Kertas dan Pensil), namun tidak perlu khawatir, soal UNBK dan UNKP pada Ujian Nasional 2018 soalnya 100% sama, jadi soal UNKP ini bisa digunakan sebagai referensi.

Berikut ini lah soal dan pembahasan UN 2018 matematika SMP/MTs Paket 4:

Download

Baca Juga:

1. Download Pembahasan UN SMP 2018 Matematika Paket 1
2. Download Naskah Asli Soal UN SMP 2018 Semua Mata Pelajaran
3. Download Naskah Asli Soal UN SMP 2017 Semua Mata Pelajaran

Demikianlah soal dan pembahasan UN (UNBK dan UNKP) Matematika SMP 2018 Paket 4 yang dapat kami bagikan. 

Jika terdapat link download yang rusak/tidak bekerja, harap beritahu kami lewat kolom komentar.

Silakan gabung di Fans Page Facebook, Channel Telegram untuk memperoleh update terbaru, dan Subscribe Channel YouTube m4th-lab untuk memperoleh video pembelajaran matematika secara gratis, untuk mengikuti tautan klik pada tombol di bawah ini:

m4th-lab Youtube Channel: 

m4th-lab Facebook Fans Page:

m4th-lab Telegram Channel:

@banksoalmatematika

Cara Merasionalkan Penyebut Bentuk Akar Pangkat Tiga Dilengkapi Soal Penerapan

Materi tentang pangkat (eksponen) dan akar sudah diperkenalkan sejak SMP, termasuk bagaimana cara merasionalkan bentuk bilangan pecahan dengan penyebut berbentuk akar. Namun sebagian besar referensi belajar yang digunakan di sekolah hanya sebatas merasionalkan bentuk akar kuadrat. Masih jarang buku yang membahas bagaimana cara merasionalkan bentuk akar pangkat tiga. Padahal, cara merasionalkan bentuk akar pangkat tiga sangat penting sebagai penunjang materi lainnya, misalnya dalam menyelesaikan limit fungsi aljabar yang memuat akar pangkat tiga tanpa menggunkan dalil L'Hopital.

Kita sudah diperkenalkan cara merasionalkan bentuk pecahan dengan penyebut akar kuadrat adalah dengan mengalikan dengan bentuk sekawannya, misalnya $\displaystyle\frac{1}{\sqrt{5}-2}$ dapat kita rasionalkan dengan mengalikannya dengan $\displaystyle\frac{\sqrt{5}+2}{\sqrt{5}+2}$ karena bentuk sekawan dari $\displaystyle \sqrt{5}-2$ adalah $\displaystyle \sqrt{5}+2$. Lalu bagaimana cara merasionalkan bentuk ini $\displaystyle\frac{3}{\sqrt[3]{5}-\sqrt[3]{2}}$?. Jika anda pikir cara merasionalkan bentuk tersebut adalah dengan mengalikannya dengan $\displaystyle\frac{\sqrt[3]{5}+\sqrt[3]{2}}{\sqrt[3]{5}+\sqrt[3]{2}}$ maka anda keliru. Untuk dapat menyelesaikannya mari kita pahami terlebih dahulu mengenai definisi dari bentuk akar sekawan berikut.

Informasi:
Tulisan pada laman ini memuat persamaan matematika yang cukup panjang dan tidak responsive pada media mobile, jika tampilan persamaan matematika di smartphone anda terpotong, silakan buka laman ini dalam mode landscape, Sangat disarankan membuka laman ini via PC/Laptop

Apa Definisi Dari Akar Sekawan?

---

Bersumber dari Ensiklopedia Matematika yang ditulis oleh ST. Nugroho dan B. Harahap, definisi dari akar sekawan adalah sebagai berikut:

Definisi Akar Sekawan
Dua bentuk akar dikatakan sekawan jika hasil kali kedua bilangan irasional (bentuk akar) adalah bilangan rasional

$\displaystyle\sqrt{a}+\sqrt{b}$ sekawan dengan $\displaystyle\sqrt{a}-\sqrt{b}$ sebab $\left(\sqrt{a}+\sqrt{b}\right)\left(\sqrt{a}-\sqrt{b}\right)=a-b$

Perhatikan beberapa contoh akar sekawan berikut:

$2-\sqrt{3}$ sekawan dengan $2+\sqrt{3}$ sebab $\left(2-\sqrt{3}\right)\left(2+\sqrt{3}\right)=4-3=1$

$\sqrt{5}+\sqrt{2}$ sekawan dengan $\sqrt{5}-\sqrt{2}$ sebab $\left(\sqrt{5}-\sqrt{2}\right)\left(\sqrt{5}+\sqrt{2}\right)=5-2=3$

$\sqrt{8}$ sekawan dengan$\sqrt{2}$, sebab $\sqrt{8}\times\sqrt{2}=\sqrt{16}=4$


Bentuk Sekawan Akar Pangkat Tiga

---

Bentuk sekawan dari $\displaystyle\sqrt[3]{a}$ adalah $\displaystyle\sqrt[3]{a^2}$, sebab:

$\begin{align*}\sqrt[3]{a}\times\sqrt[3]{a^2}&=a^{\frac{1}{3}}\times a^{\frac{2}{3}}\\&=a^{\frac{1}{3}+\frac{2}{3}}\\&=a^{\frac{3}{3}}\\&=a^1\\&=a\end{align*}$

Sekarang, bagaimana bentuk akar sekawan dari $\displaystyle\sqrt[3]{a}+\sqrt[3]{b}$?
Bentuk akar sekawan dari bentuk di atas pastinya harus menyebabkan "muncul" pangkat tiga pada kedua suku bentuk akar di atas, bentuk aljabar sebagai landasan yang akan kita gunakan adalah sebagai berikut:

$\begin{align*}x^3-y^3&=(x-y)(x^2+xy+y^2)\\x^3+y^3&=(x+y)(x^2-xy+y^2)\end{align*}$

Contoh, akar sekawan dari $\displaystyle\sqrt[3]{5}-\sqrt[3]{2}$ adalah $\displaystyle\left(\sqrt[3]{5}\right)^2+\sqrt[3]{5}.\sqrt[3]{2}+\left(\sqrt[3]{2}\right)^2$ atau bisa juga ditulis $\displaystyle\sqrt[3]{25}+\sqrt[3]{10}+\sqrt[3]{4}$ sebab:

$\begin{align*}\left(\sqrt[3]{5}-\sqrt[3]{2}\right)\left(\sqrt[3]{25}+\sqrt[3]{10}+\sqrt[3]{4}\right)&=\left(\sqrt[3]{5}\right)^3-\left(\sqrt[3]{2}\right)^3\\&=5-2\\&=3\end{align*}$

Berikut ini bentuk-bentuk akar sekawan akar pangkat tiga:

Bentuk sekawan dari $\displaystyle\sqrt[3]{a}$ adalah $\displaystyle\sqrt[3]{a^2}$

Bentuk sekawan dari $\displaystyle\sqrt[3]{a}-\sqrt[3]{b}$ adalah $\displaystyle\sqrt[3]{a^2}+\sqrt[3]{ab}+\sqrt[3]{b^2}$

Bentuk sekawan dari $\displaystyle\sqrt[3]{a}+\sqrt[3]{b}$ adalah $\displaystyle\sqrt[3]{a^2}-\sqrt[3]{ab}+\sqrt[3]{b^2}$

Bentuk sekawan dari $\displaystyle a-\sqrt[3]{b}$ adalah $\displaystyle a^2+a\sqrt[3]{b}+\sqrt[3]{b^2}$

 Bentuk sekawan dari $\displaystyle a+\sqrt[3]{b}$ adalah $\displaystyle a^2-a\sqrt[3]{b}+\sqrt[3]{b^2}$

Bentuk sekawan dari $\displaystyle \sqrt[3]{a}-b$ adalah $\displaystyle\sqrt[3]{a^2}+b\sqrt[3]{a}+b^2$

 Bentuk sekawan dari $\displaystyle \sqrt[3]{a}+b$ adalah $\displaystyle\sqrt[3]{a^2}-b\sqrt[3]{a}+b^2$

Merasionalkan Penyebut Akar Pangkat Tiga

---

Setelah mengetahui bentuk sekawan akar pangkat tiga, sekarang kita akan menggunakan bentuk sekawan tersebut untuk merasionalkan penyebut akar pangkat tiga, perhatikan beberapa contoh di bawah ini:

Contoh 1

Bentuk rasional dari $\displaystyle\frac{9}{2\sqrt[3]{2}}$ adalah ....

Jawab:
Bentuk akar sekawan dari $\sqrt[3]{2}$ adalah $\sqrt[3]{4}$
$\begin{align*}\frac{9}{2\sqrt[3]{2}}\times\frac{\sqrt[3]{4}}{\sqrt[3]{4}}&=\frac{9\sqrt[3]{4}}{2\times 2}\\&=\frac{9}{4}\sqrt[3]{4}\end{align*}$

Contoh 2

Bentuk rasional dari $\displaystyle\frac{5}{\sqrt[3]{7}-\sqrt[3]{2}}$ adalah ....

Jawab:

Bentuk akar sekawan dari $\sqrt[3]{7}-\sqrt[3]{2}$ adalah $\sqrt[3]{49}+\sqrt[3]{14}+\sqrt[3]{4}$ maka:

$\begin{align*}\frac{5}{\sqrt[3]{7}-\sqrt[3]{2}}\times\frac{\sqrt[3]{49}+\sqrt[3]{14}+\sqrt[3]{4}}{\sqrt[3]{49}+\sqrt[3]{14}+\sqrt[3]{4}}&=\frac{5\left(\sqrt[3]{49}+\sqrt[3]{14}+\sqrt[3]{4}\right)}{7-2}\\&=\frac{5\left(\sqrt[3]{49}+\sqrt[3]{14}+\sqrt[3]{4}\right)}{5}\\&=\sqrt[3]{49}+\sqrt[3]{14}+\sqrt[3]{4}\end{align*}$

Contoh 3

Bentuk rasional dari $\displaystyle\frac{\sqrt[3]{2}}{\sqrt[3]{2}+1}$ adalah ....

Jawab:

Bentuk akar sekawan dari $\sqrt[3]{2}+1$ adalah $\sqrt[3]{4}-\sqrt[3]{2}+1$

$\begin{align*}\frac{\sqrt[3]{2}}{\sqrt[3]{2}+1}\times\frac{\sqrt[3]{4}-\sqrt[3]{2}+1}{\sqrt[3]{4}-\sqrt[3]{2}+1}&=\frac{\sqrt[3]{2}\left(\sqrt[3]{4}-\sqrt[3]{2}+1\right)}{2+1}\\&=\frac{\sqrt[3]{8}-\sqrt[3]{4}+\sqrt[3]{2}}{3}\\&=\frac{2-\sqrt[3]{4}+\sqrt[3]{2}}{3}\\&=\frac{1}{3}\left(2-\sqrt[3]{4}+\sqrt[3]{2}\right)\end{align*}$



Contoh Penerapan dalam Menyelesaikan Masalah Limit

---

Berikut ini contoh soal limit yang melibatkan akar pangkat tiga,

$\displaystyle\lim_{x\to 8}\frac{x-8}{\sqrt[3]{x}-2}=$ ....

Jika kita substitusi langsung $x=8$, maka akan kita peroleh bentuk tak tentu $\displaystyle\frac{0}{0}$, dengan demikin diperlukan manupulasi aljabar untuk menyelesaikannya dengan cara menghilangkan faktor persekutuan pembilang dan penyebut yang menyebabkan nilai $\displaystyle\frac{0}{0}$.

Bentuk akar sekawan dari $\sqrt[3]{x}-2$ adalah $\sqrt[3]{x^2}+2\sqrt[3]{x}+4$, dan $\left(\sqrt[3]{x}-2\right)\left(\sqrt[3]{x^2}+2\sqrt[3]{x}+4\right)=x-8$ maka:

$\begin{align*}\lim_{x\to 8}\frac{x-8}{\sqrt[3]{x}-2}\times\frac{\sqrt[3]{x^2}+2\sqrt[3]{x}+4}{\sqrt[3]{x^2}+2\sqrt[3]{x}+4}&=\lim_{x\to 8}\frac{(x-8)(\sqrt[3]{x^2}+2\sqrt[3]{x}+4)}{x-8}\\&=\lim_{x\to 8}\sqrt[3]{x^2}+2\sqrt[3]{x}+4\\&=\sqrt[3]{64}+2\sqrt[3]{8}+4\\&=4+4+4\\&=12\end{align*}$

Demikianlah cara merasionalkan penyebut akar pangkat tiga yang dapat saya bahas. 
Semoga bermanfaat